神经网络算法是一种受生物神经系统启发而构建的机器学习模型，广泛应用于模式识别、分类、回归等任务。其核心思想是利用大量的简单计算单元（神经元）相互连接形成网络，通过数据学习来实现复杂的非线性映射关系。

    神经网络算法是一种受生物神经系统启发而构建的机器学习模型，广泛应用于模式识别、分类、回归等任务。其核心思想是利用大量的简单计算单元（神经元）相互连接形成网络，通过数据学习来实现复杂的非线性映射关系。

神经网络的基本结构

基本构成


一个典型的神经网络由多个层级组成，包括输入层、隐藏层和输出层。每一层由若干神经元构成，这些节点通过权重相连接。


神经网络通过调整这些权重，学习输入数据与输出结果之间的映射关系。




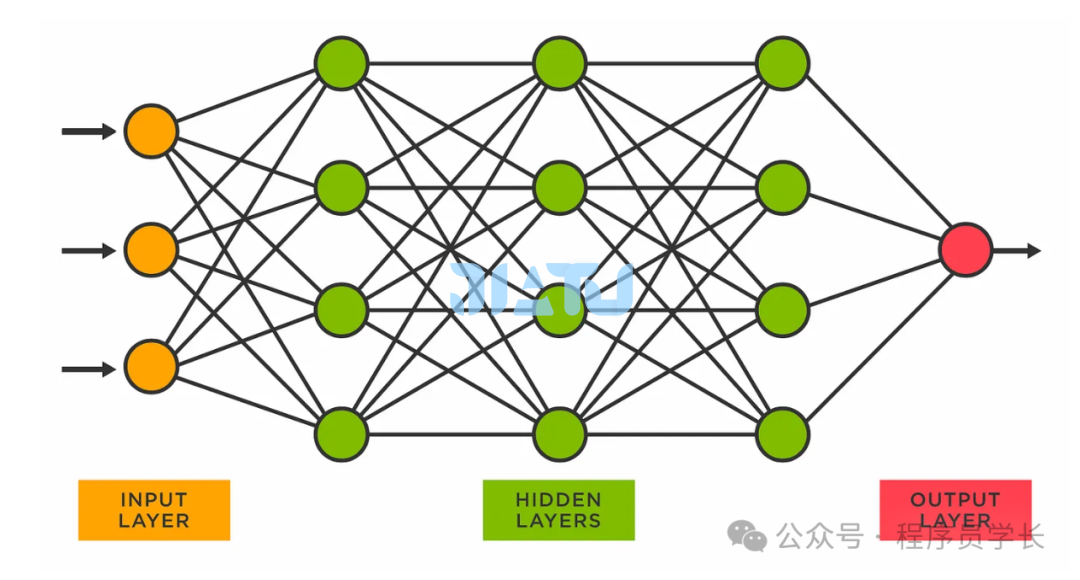
  • 输入层

    接收外部数据，每个神经元对应输入数据的一个特征。

  • 隐藏层

    位于输入层和输出层之间，负责特征提取和表示。
    一个神经网络可以有多个隐藏层，隐藏层的层数和每层神经元数量可以根据具体任务调整。

  • 输出层

    生成最终的预测结果，如分类标签或回归值。
    神经元数量依据具体任务而定（例如，分类任务中的类别数）。

神经元


神经网络的基本组成单位是神经元。


每个神经元接收来自前一层神经元的输入信号，通过加权求和后，然后经过一个激活函数，产生输出信号传递到下一层神经元。







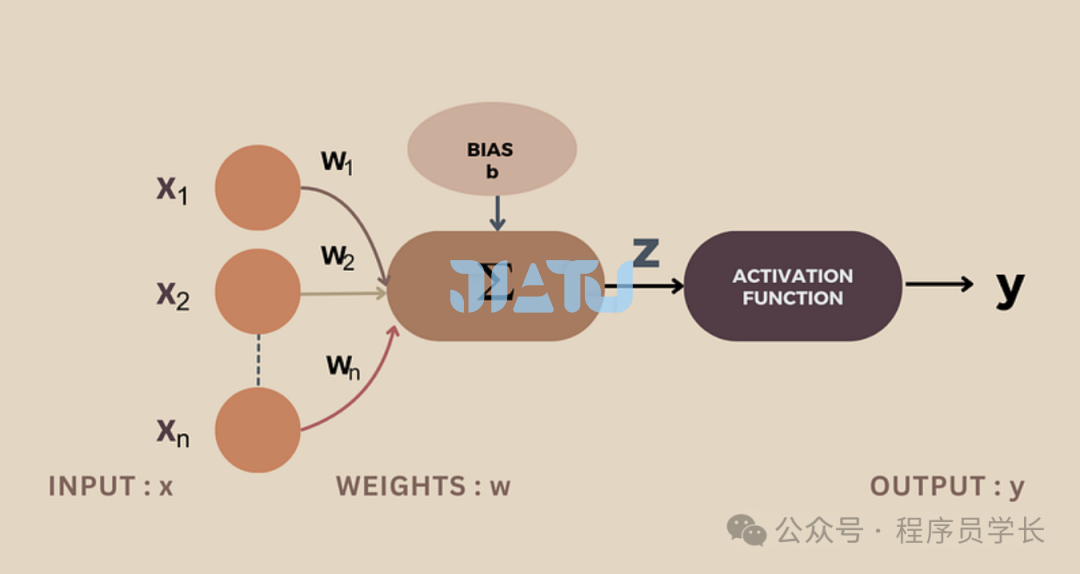
其中：

  • 为输入信号
  • 是对应的权重
  • b 是偏置
  • z 为加权和


将线性输出结果 z 通过激活函数 转化为非线性输出



激活函数


激活函数是神经网络中的重要组成部分，它引入非线性，使神经网络能够处理复杂的非线性问题
常见的激活函数包括：


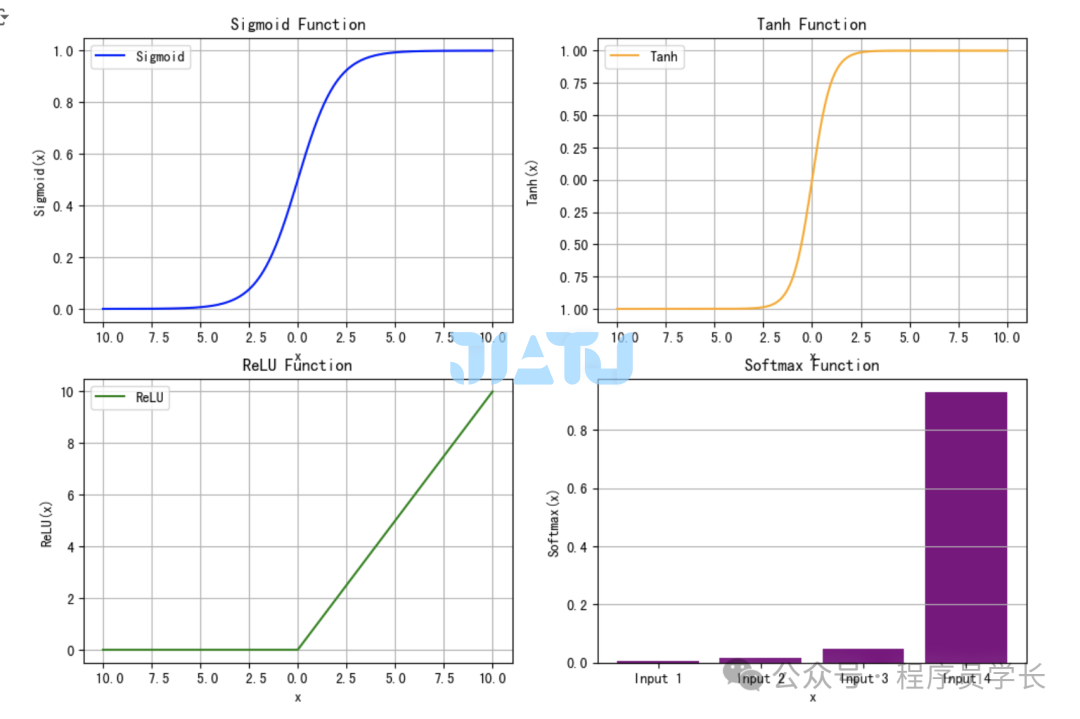
  • Sigmoid 函数

    将输入映射到 0 和 1 之间，适合二分类问题输出概率。

  • Tanh

    类似于 Sigmoid，但输出范围中心对称，更适合处理零均值数据。

  • ReLU

    简单高效，对正值保持线性，对负值截断为 0。

  • Softmax 激活函数

    将输入向量转换为概率分布。
import numpy as np
import matplotlib.pyplot as plt

# 定义激活函数
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

def tanh(x):
    return np.tanh(x)

def relu(x):
    return np.maximum(0, x)

def softmax(x):
    e_x = np.exp(x - np.max(x)) 
    return e_x / e_x.sum(axis=0)


x = np.linspace(-10, 10, 500)
sigmoid_y = sigmoid(x)
tanh_y = tanh(x)
relu_y = relu(x)

softmax_input = np.array([1.0, 2.0, 3.0, 6.0])
softmax_y = softmax(softmax_input)

# 绘制 Sigmoid
plt.figure(figsize=(12, 8))
plt.subplot(2, 2, 1)
plt.plot(x, sigmoid_y, label="Sigmoid", color="blue")
plt.title("Sigmoid Function")
plt.xlabel("x")
plt.ylabel("Sigmoid(x)")
plt.grid()
plt.legend()

# 绘制 Tanh
plt.subplot(2, 2, 2)
plt.plot(x, tanh_y, label="Tanh", color="orange")
plt.title("Tanh Function")
plt.xlabel("x")
plt.ylabel("Tanh(x)")
plt.grid()
plt.legend()

# 绘制 ReLU
plt.subplot(2, 2, 3)
plt.plot(x, relu_y, label="ReLU", color="green")
plt.title("ReLU Function")
plt.xlabel("x")
plt.ylabel("ReLU(x)")
plt.grid()
plt.legend()

# 绘制 Softmax 的柱状图
plt.subplot(2, 2, 4)
categories = [f"Input {i+1}" for i in range(len(softmax_input))]
plt.bar(categories, softmax_y, color="purple")
plt.title("Softmax Function")
plt.xlabel("x")
plt.ylabel("Softmax(x)")
plt.grid(axis="y")
plt.show()



神经网络的训练过程

神经网络的训练过程主要包括前向传播、损失计算、反向传播和参数更新。



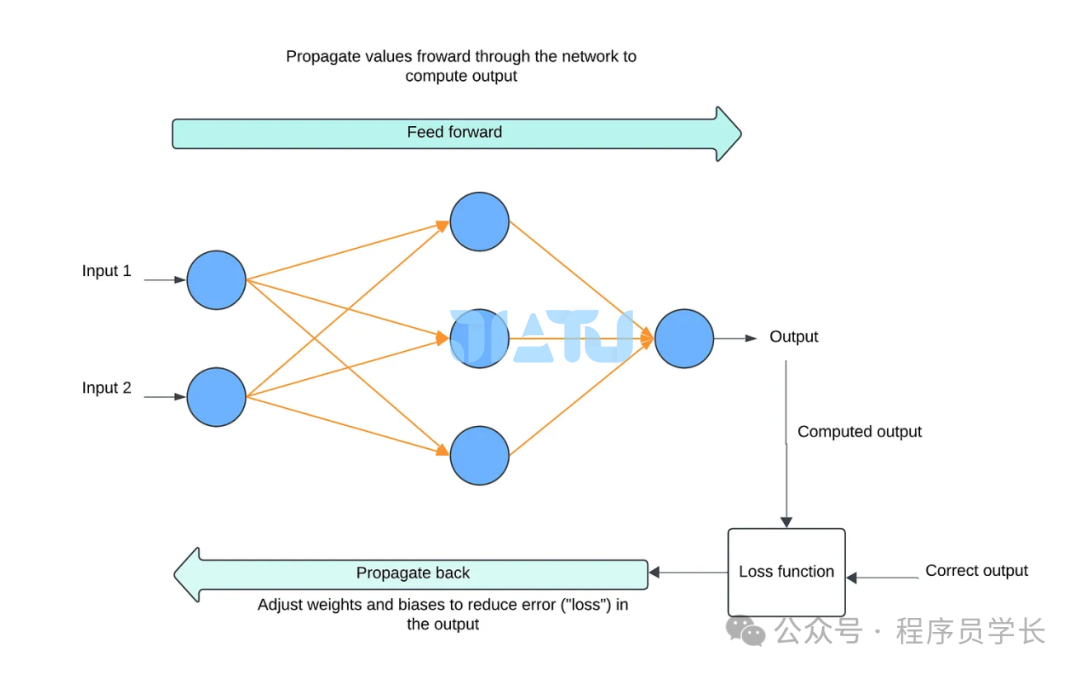
前向传播


前向传播是指输入数据通过网络层层传递，最终产生输出的过程。
对于一个包含多层的前馈神经网络，前向传播的数学表示为：
对于第 lll 层的神经元：




其中：

  • 为第 层的权重矩阵
  • 为第 层的激活值
  • 为第 层的偏置向量
  • 为激活函数

损失函数


损失函数用于衡量神经网络输出与真实标签之间的差距，常见的损失函数有均方误差（MSE）和交叉熵损失（Cross-Entropy Loss）。


均方误差 (MSE)


用于回归问题。



交叉熵损失

用于分类问题。

其中 y 为真实值， 为预测值，m 为样本数。


反向传播和权重更新


反向传播是神经网络训练的核心，通过计算损失函数对各层权重的梯度，然后使用梯度下降算法调整权重以最小化损失函数。


  1. 输出层误差

    首先计算输出层的误差，即损失函数对输出层激活值的偏导数

  2. 隐藏层误差

    对于隐藏层的神经元，误差由上一层传播过来，通过链式法则计算。
    对于第 l 层，误差为：

  3. 梯度计算

    反向传播中，我们计算每一层的权重和偏置的梯度

  4. 权重更新

    通过反向传播计算得到每一层权重和偏置的梯度后，使用梯度下降法等优化算法来更新参数。
    其中， 是学习率，控制每次更新的步长

通过多次迭代前向传播和反向传播，神经网络能够逐步找到最优的权重和偏置，最终实现较高的预测精度。


案例分享


下面是一个使用神经网络对鸢尾花数据集进行分类的示例代码，分别用 TensorFlow 和 PyTorch 进行实现。


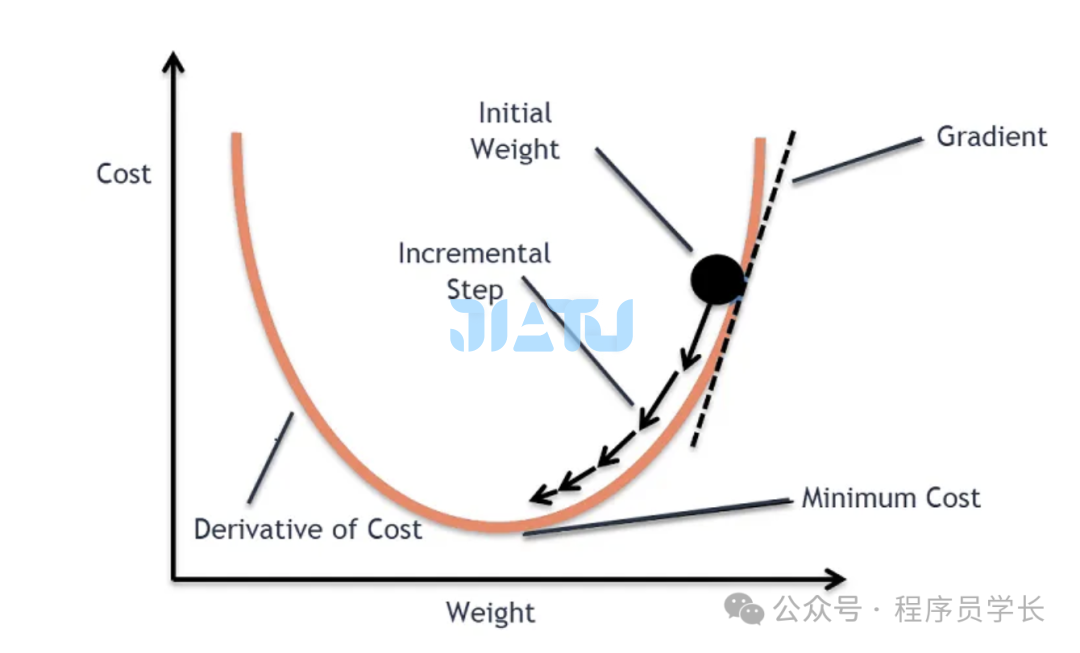
TensorFlow 实现

import tensorflow as tf
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder
import matplotlib.pyplot as plt

iris = load_iris()
X = iris.data
y = iris.target

scaler = StandardScaler()
X = scaler.fit_transform(X)

encoder = OneHotEncoder(sparse_output=False)
y = encoder.fit_transform(y.reshape(-1, 1))

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 构建神经网络模型
model = tf.keras.Sequential([
    tf.keras.layers.Dense(16, activation='relu', input_shape=(4,)),
    tf.keras.layers.Dense(3, activation='softmax')
])

model.compile(optimizer='adam', loss='categorical_crossentropy', metrics=['accuracy'])

# 训练模型
history = model.fit(X_train, y_train, epochs=100, batch_size=16, validation_data=(X_test, y_test), verbose=1)

# 绘制损失函数图像
plt.plot(history.history['loss'], label='Train Loss')
plt.plot(history.history['val_loss'], label='Validation Loss')
plt.xlabel('Epoch')
plt.ylabel('Loss')
plt.title('Training Loss (TensorFlow)')
plt.legend()
plt.show()



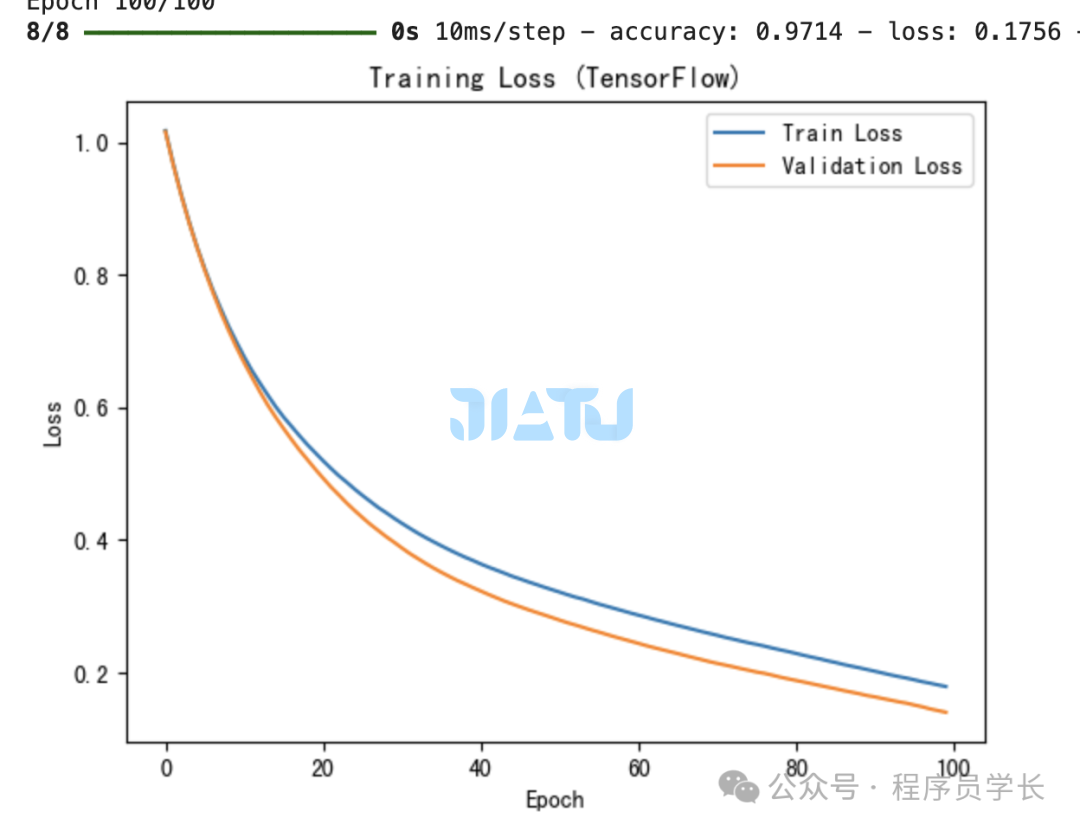
PyTorch 实现

import torch
import torch.nn as nn
import torch.optim as optim
from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler, OneHotEncoder
import matplotlib.pyplot as plt

iris = load_iris()
X = iris.data
y = iris.target

scaler = StandardScaler()
X = scaler.fit_transform(X)

encoder = OneHotEncoder(sparse_output=False)
y = encoder.fit_transform(y.reshape(-1, 1))

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)

# 转换为张量
X_train = torch.tensor(X_train, dtype=torch.float32)
X_test = torch.tensor(X_test, dtype=torch.float32)
y_train = torch.tensor(y_train, dtype=torch.float32)
y_test = torch.tensor(y_test, dtype=torch.float32)

# 定义神经网络模型
class NeuralNetwork(nn.Module):
    def __init__(self):
        super(NeuralNetwork, self).__init__()
        self.fc1 = nn.Linear(4, 16)
        self.fc2 = nn.Linear(16, 3)
        self.relu = nn.ReLU()

    def forward(self, x):
        x = self.relu(self.fc1(x))
        x = self.fc2(x)
        return x

model = NeuralNetwork()

# 定义损失函数和优化器
criterion = nn.CrossEntropyLoss()
optimizer = optim.Adam(model.parameters(), lr=0.01)

# 训练模型
losses = []
epochs = 100
for epoch in range(epochs):
    optimizer.zero_grad()
    outputs = model(X_train)
    loss = criterion(outputs, torch.argmax(y_train, axis=1))
    loss.backward()
    optimizer.step()
    losses.append(loss.item())

    if (epoch + 1) % 10 == 0:
        print(f"Epoch [{epoch + 1}/{epochs}], Loss: {loss.item():.4f}")

# 绘制损失函数图像
plt.plot(range(epochs), losses)
plt.xlabel('Epoch')
plt.ylabel('Loss')
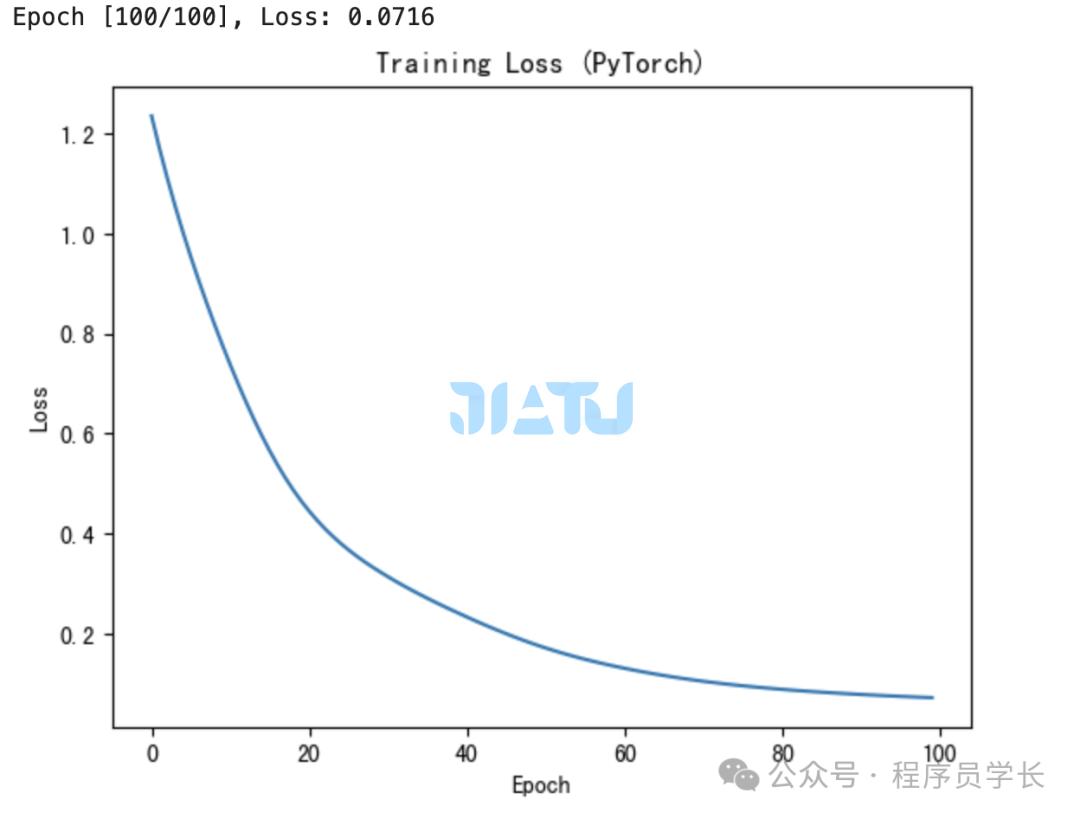
plt.title('Training Loss (PyTorch)')
plt.show()